Momentum

A technique used when minimizing a function using gradient descent that helps avoid local minima.

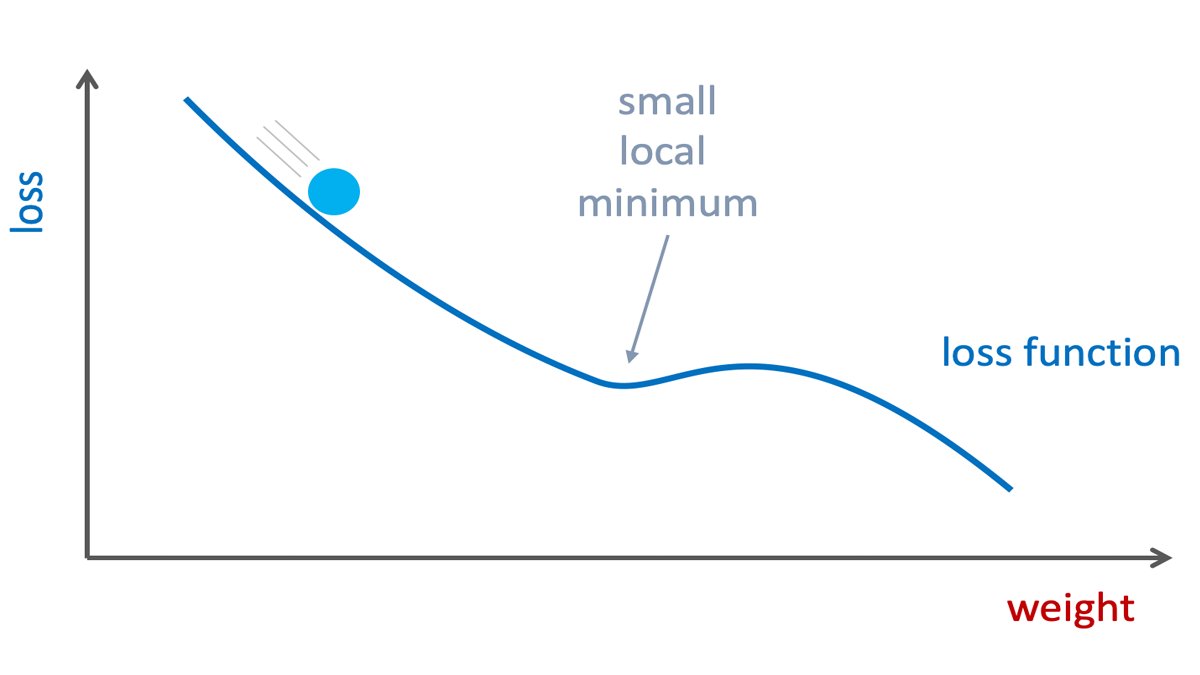
One of the biggest problems when using gradient descent to minimize a function is that the optimization process may get stuck in a local minimum. Momentum is a technique that tries to mitigate that by allowing the optimization to "gather speed" and jump over small "hills" in the function.

Detailed formula explanation

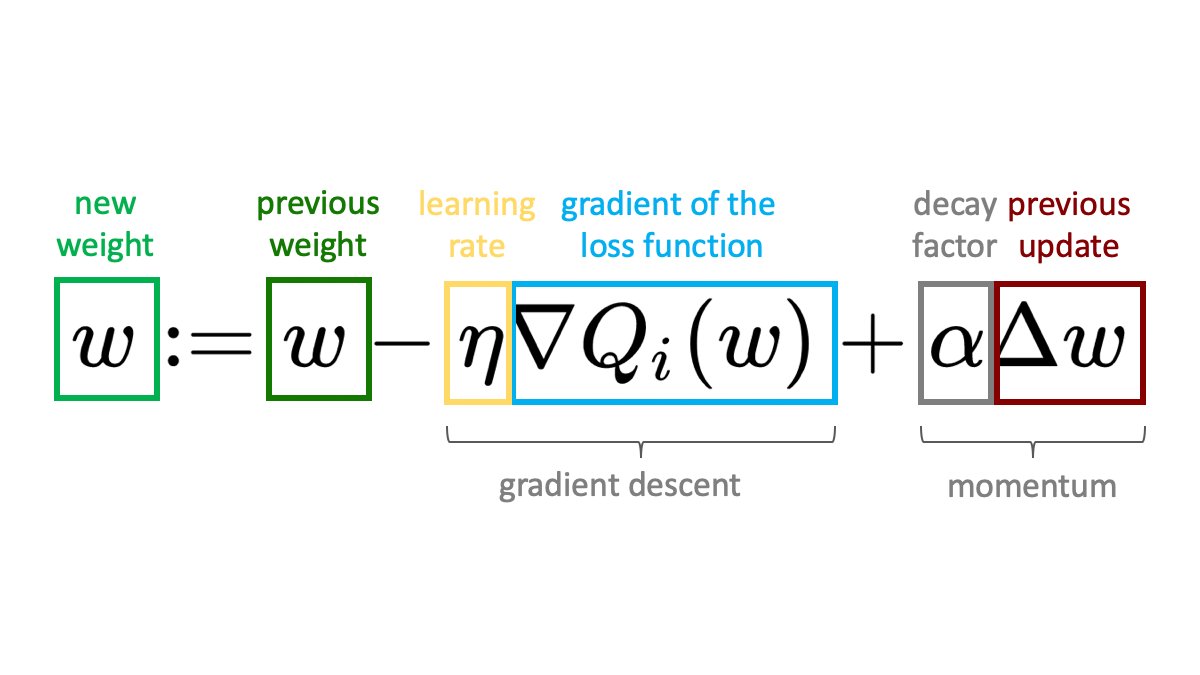
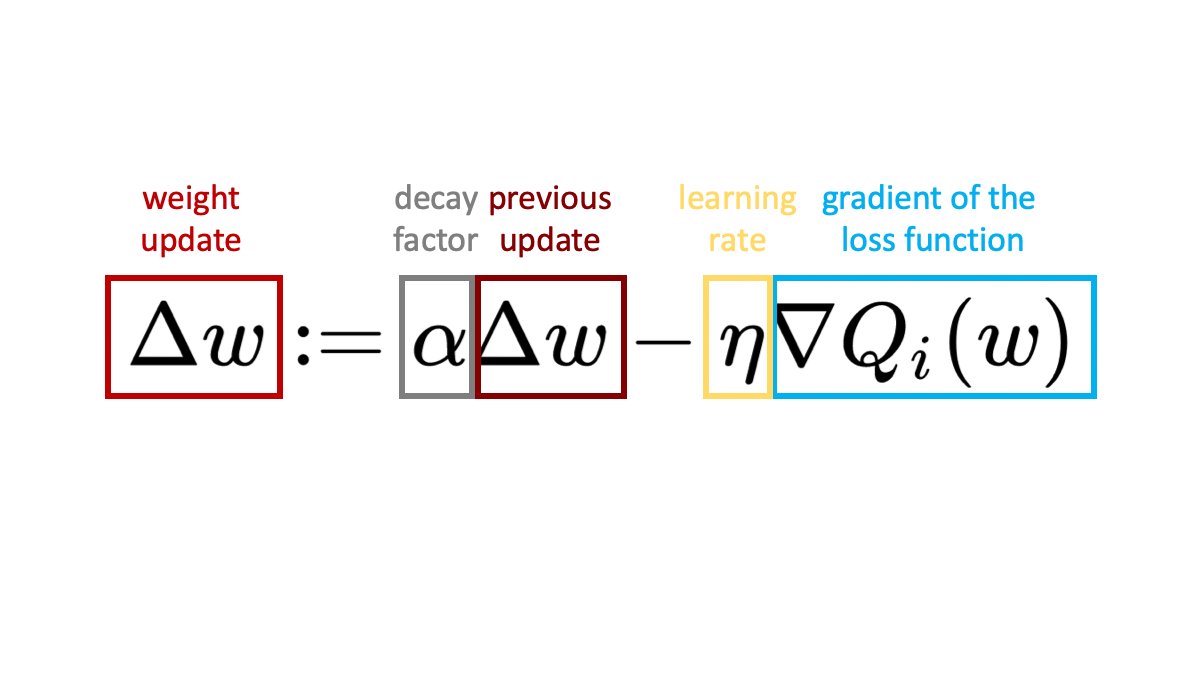
The formulat for momentum used in a gradient descent optimization can be written as:

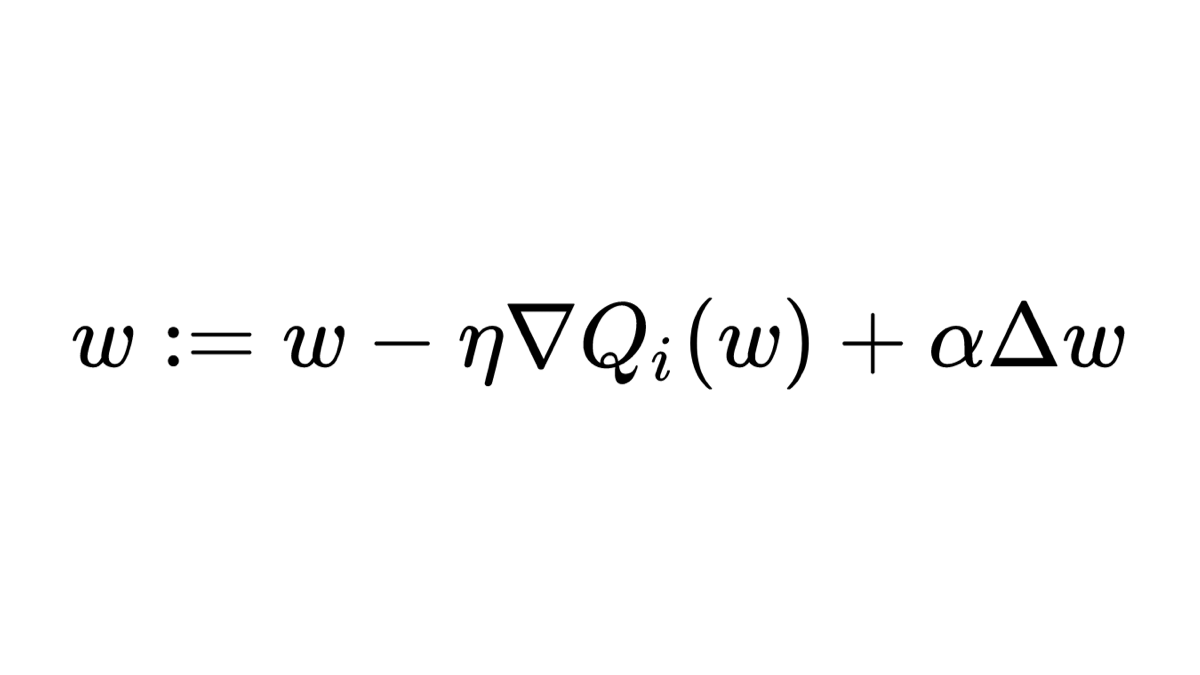
The formula is based on a simple iterative optimization algorithm, that can be expressed as:

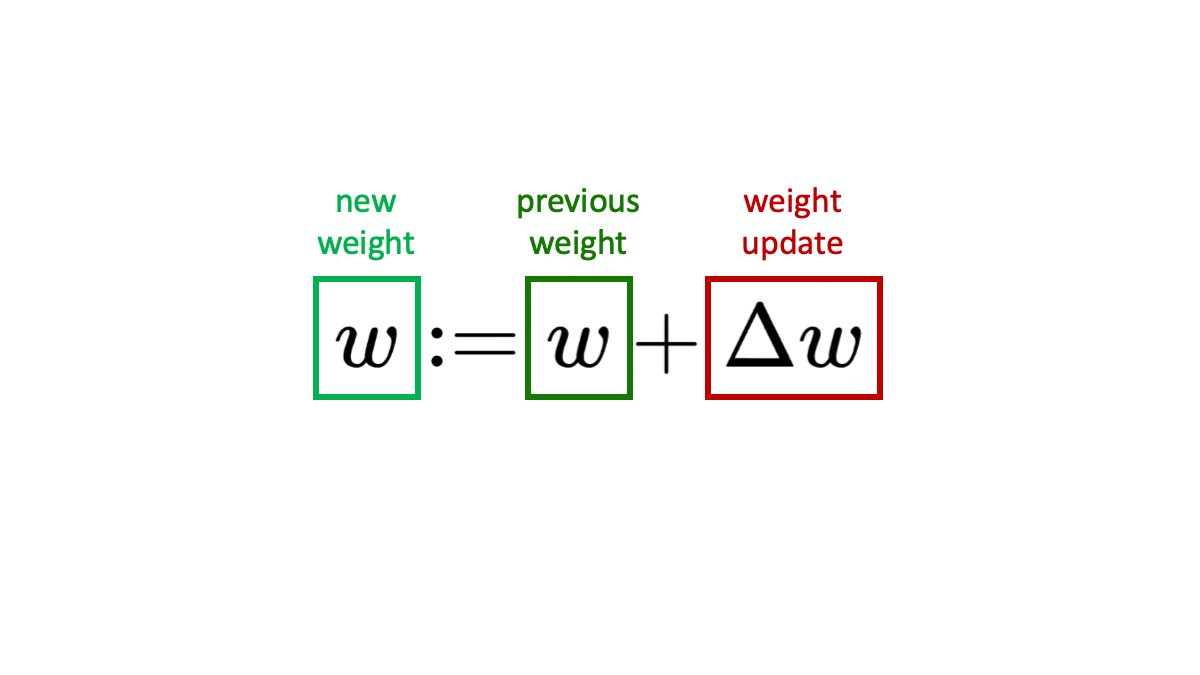
In a simple gradient descent optimization, we define the update of the weights as:

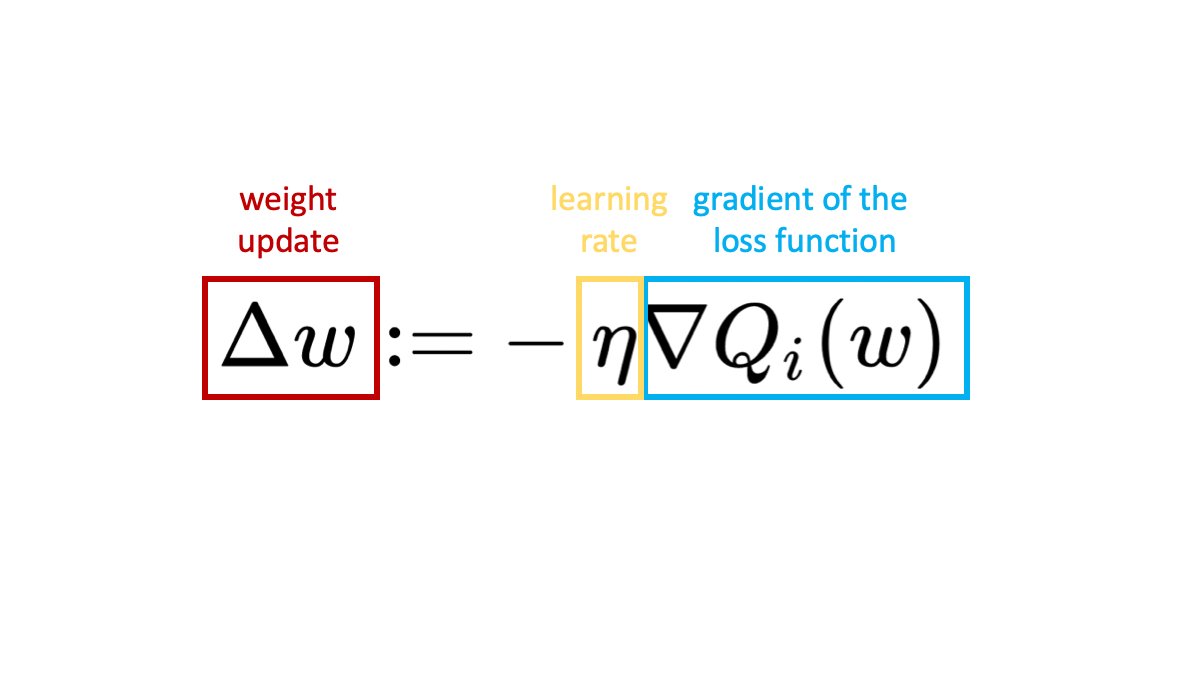
If we want to add momentum, we add an additional term - the weight update in the previous step times a decay factor. The decay factor α is just a number between 0 and 1 defining how much of the previous update will be taken into account. If we set α = 0 then no momentum is applied, while α = 1 means a lot of momentum.

A useful analogy is a ball rolling down a hill. If the hill is steep, the ball will accelerate (we update the weights more). This will help the ball jump over small local minima and continue down the hill (to a smaller value of the function). More momentum means a heavier ball with higher inertia.

The final formula of gradient descent optimization with momentum becomes: